Unsupervised Hierarchical Part-based Decomposition

Here the infant shows an intuitive understanding of symbolic object manipulation, by stacking cups based on their size (video source).

Within the first year of their life, humans develop a common-sense understanding of the physical behaviour of the world. For example, we are able to identify 3D objects in a scene and infer their geometric and physical properties, even when these objects are partially visible. We can reason about intentions and perform judgments based on our interaction with the world.

Here the toddler understands the intention of an agent and decides to interact with its environment and help the agent (video source).

Likewise, 3D scene understanding is a fundamental task for a great variety of computer vision applications. Existing algorithms are primarily focused on single 3D object reconstruction and thus cannot generalize to complex scenes with multiple objects. However, the big question is whether existing representations are sufficient for capturing information beyond single object 3D reconstruction such as relationship between objects, interactions, events or higher level concepts?

Here the baby reaches back for an object that they haven't touched for a while. This spatial-object understanding is called Object Permanence and humans seem to have this capability as early as five months (video source).

Structure-aware representations

Our understanding of the world relies heavily on the ability to properly reason about the arrangement of objects in a scene. Early works in cognitive science stipulate that the human visual system perceives objects as a hierarchical decomposition of parts. Interestingly, while this seems to be a fairly easy task for the human brain, computer vision algorithms struggle to form such a high-level reasoning, particularly in the absence of supervision.

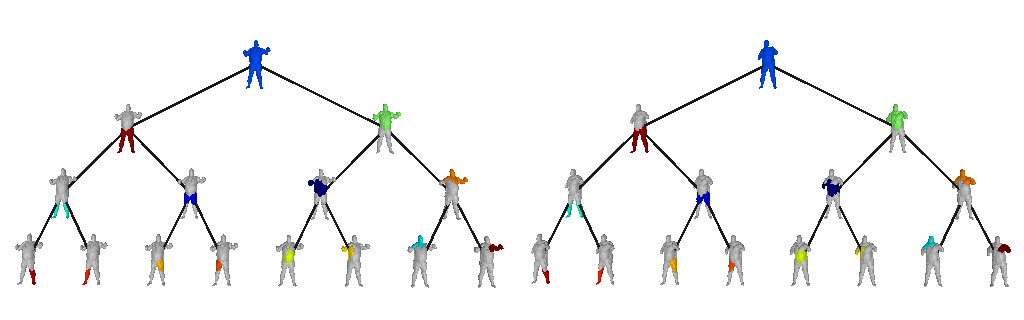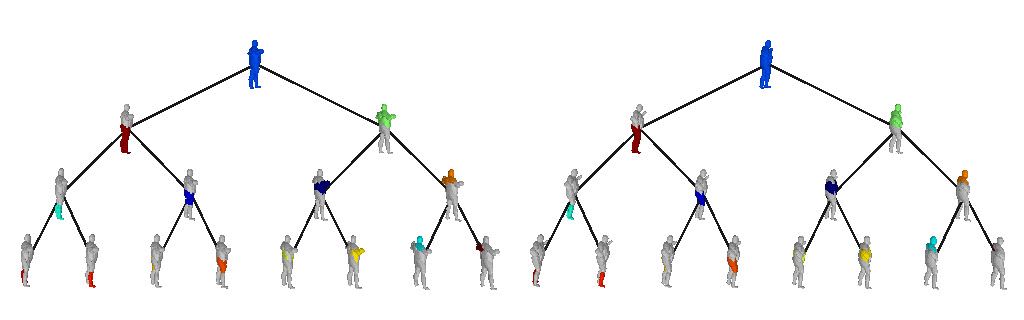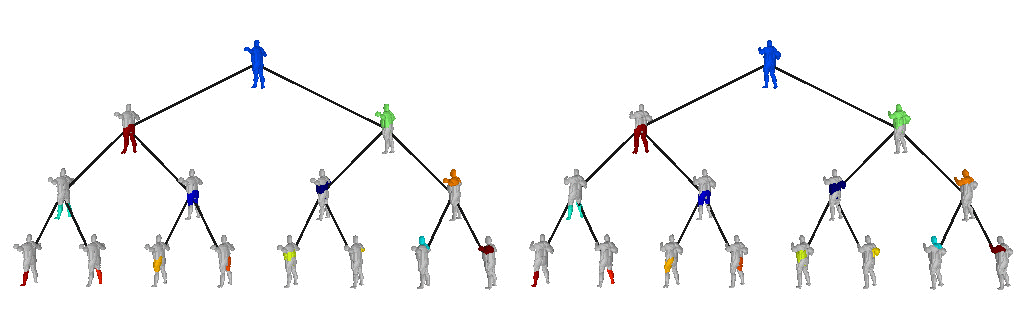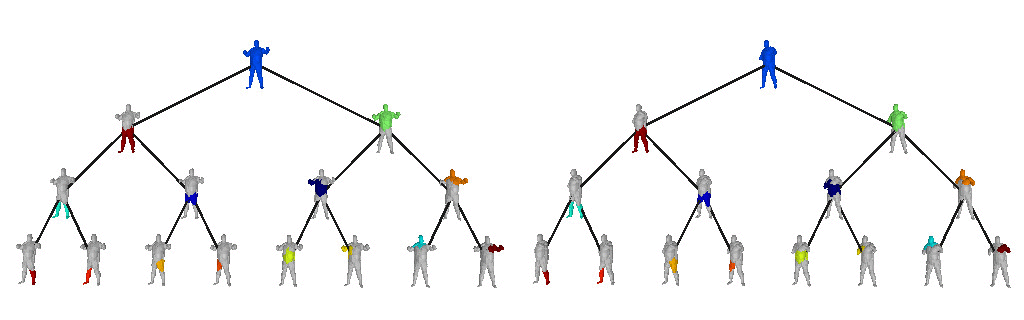
The structure of a scene is tightly related to the inherent hierarchical organization of its parts. At a coarse level, a scene can be decomposed into objects and at a finer level each object can be represented with parts and these parts with finer parts. Take the human body for example. It can be decomposed into upper and lower body. The lower body can be subsequently decomposed into two legs. These legs cab be decomposed into thighs and legs, each of which can be subsequently decomposed into even finer parts.

Deep learning led to impressive progress in 3D reconstruction by learning a parametric function, implemented as a neural network that maps an input image to a 3D shape represented as a mesh, a pointcloud, a voxel grid or a set of primitives.

However, existing shape representations focus primarily on recovering the local 3D geometry of an object without considering its latent hierarchical layout of semantic parts. To this end, we propose a structure-aware representation that considers part relationships and models object parts with multiple levels of abstraction, namely geometrically complex parts are modeled with more components and simple parts are modeled with fewer components.

In a nutshell

Our structure-aware representation is based on the simple assumption that complex object parts should be modelled with more primitives, whereas geometrically simpler parts with fewer components. In contrast to existing primitive-based techniques that represent 3D objects as an unstructured collection of parts, we employ a neural network that learns to recursively decompose an object into its constituent parts by building a latent space that encodes both the part-level hierarchy and the part geometries. The hierarchical decomposition is represented as an unbalanced binary tree of primitives of depth \(D\).

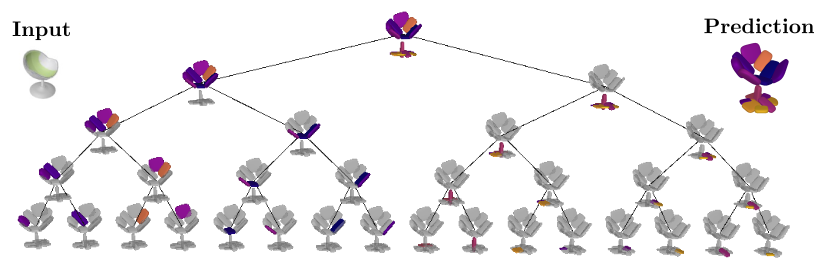
At every depth level, each of the $2^d \mid d={0, \dots, D}$ nodes is recursively split into two nodes (its children) until reaching the maximum depth. This results in a representation with various levels of detail. Naturally, reconstructions from deeper depth levels are more detailed. Note that the reconstructions below are derived from the same model, trained with a maximum number of \(2^4 = 16\) primitives. During inference, the network dynamically combines representations from different depth levels to recover the final prediction.

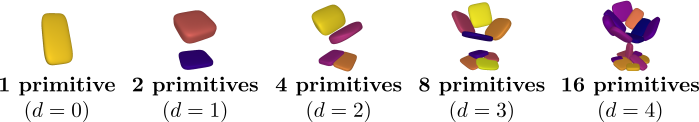
More importantly, the hierarchical part-based decomposition is learned without any supervision neither on the object parts nor their structure. Instead, our model jointly infers these latent variables during training. Learning the hierarchical decomposition of an object allows us to:

• Model relationships between parts.
• Model correspondences across parts.
• Have a multi-scale representation that can be efficiently stored at the required level of detail (namely with less parameters).
• Improve the reconstruction quality by modelling different parts of an object with different levels of abstraction.

How do we learn such a model?

Our Approach

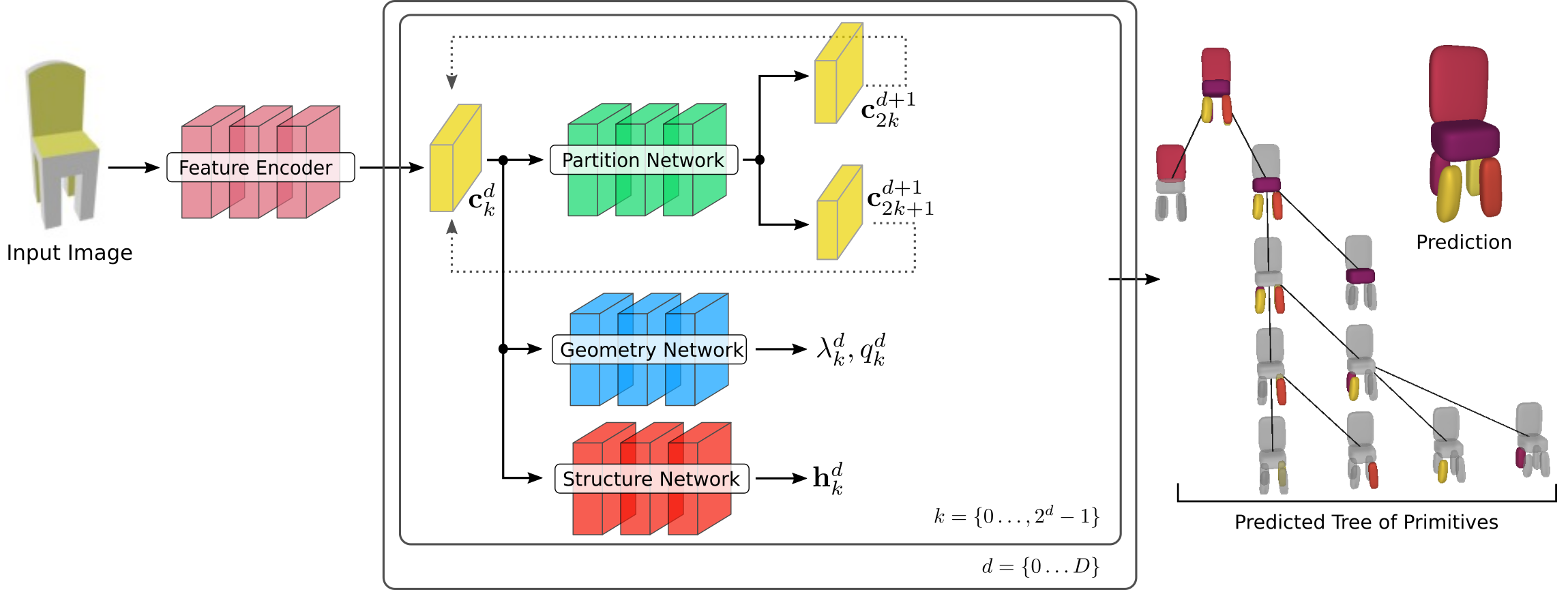
Given an input image/shape \(\mathbf{I}\) and a set of pairs \(\mathbf{X} = \{\left(\mathbf{x_i}, o_i\right)\}_{i=1}^N\) that represent the target object, we predict a hierarchical decomposition over parts in the form of a binary tree of primitives of depth \(D\) as

\[\mathbf{P}=\{\{p_k^d\}_{k=0}^{2^d-1} \,\mid \, d=\{0\dots D\}\}\]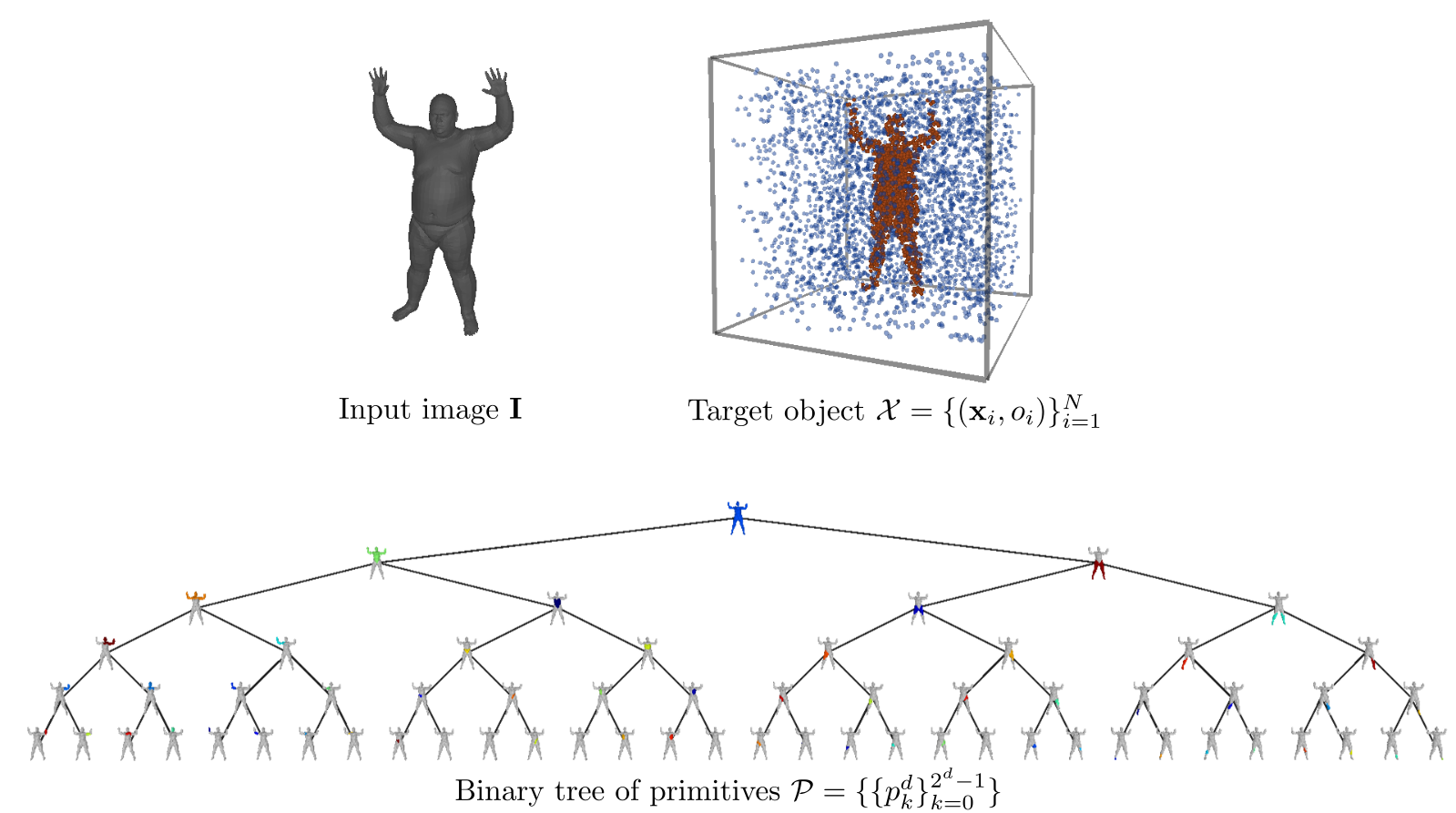

At every depth level, $\mathbf{P}$ reconstructs the target object with \(\{1,2,\dots, M\}\) primitives, where $M$ is an upper limit to the maximum number of primitives and is equal to \(2^D\). More specifically, \(\mathbf{P}\) is constructed as follows: the root node is associated with the root primitive that represents the entire shape and is recursively split into two nodes (its children) until reaching the maximum depth \(D\). This recursive partition yields reconstructions that recover the geometry of the target shape using \(2^d\) primitives at each depth level, where $d$ denotes the depth level.

For each primitive \(p_k^d\) our network regresses a set of parameters \(\lambda_k^d\) that define its shape, size and position in 3D space and its reconstruction quality \(q_k^d\). Based on the value of \(q_k^d\) the network dynamically stops the recursive partitioning process, resulting in unbalanced tree of primitives. We formulate the per-primitive occupancy function \(g:\mathbb{R}^3 \rightarrow [0, 1]\), using its distance function \(f(\mathbf{x}, \lambda)\) as:

\[g(\mathbf{x}; \lambda) = \sigma\left(s\left(1 - f(\mathbf{x}; \lambda)^{\epsilon_1}\right)\right)\]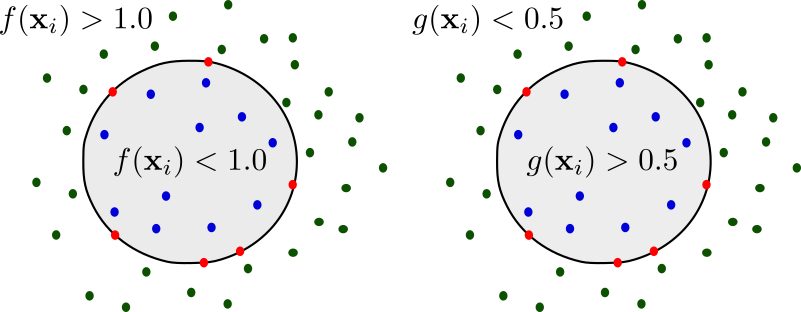

The occupancy function of the assembled shape at depth \(d\) \(G^d(\mathbf{x})\), using $2^d$ primitives, is simply their intersection and can be approximated by taking the max of the occupancy functions of all primitives

\[G^d(\mathbf{x}) = \max_{\substack{k \in 0\dots2^d-1}}g_k^d\left(\mathbf{x}; \lambda_k^d\right)\]

During training, our network learns to predict shapes that contain all internal points from the target mesh \((o_i=1)\) and none of the external \((o_i=0)\). Our network comprises three main components:

• the partition network that recursively splits the shape representation into representations of parts,
• the structure network that learns the hierarchical arrangement of primitives, namely assigning parts of the object to the primitives at each depth level
• the geometry network that recovers the primitive parameters and the reconstruction quality of each primitive.

Our optimization objective is a weighted sum over four terms:

• Structure loss enforces the hierarchical tree decomposition.
• Reconstruction loss measures how well the predicted shape matches the target shape.
• Compatibility loss measures how good each primitive fits the object part it represents.
• Proximity loss acts as regularizer to counteract the vanishing gradients.

How well does it work?

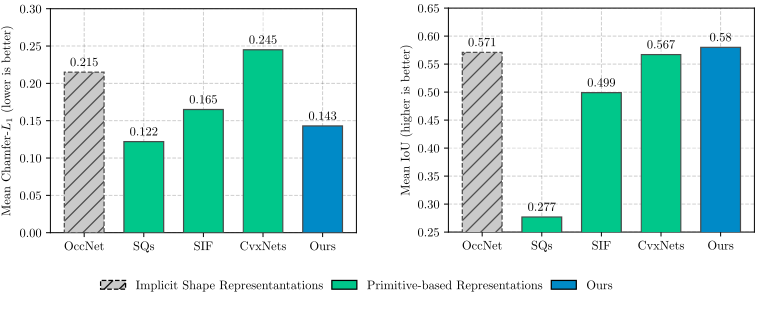
Experiments on ShapeNet and Dynamic FAUST demonstrate that our structure-aware representation is able to model different parts of the object with different levels of abstraction, thus leading to more expressive and geometrically accurate compared to approaches that only consider the 3D geometry of the object parts.

Our model yields geometrically accurate reconstructions that outperform existing primitive-based methods, while performing competitively with more flexible implicit shape representations.

Below we visualize the predicted tree of primitives on various ShapeNet objects. We observe that our model recovers unbalanced binary trees that decompose a 3D object into a set of parts. We associate every primitive with a unique color, thus primitives illustrated with the same color correspond to the same object part.

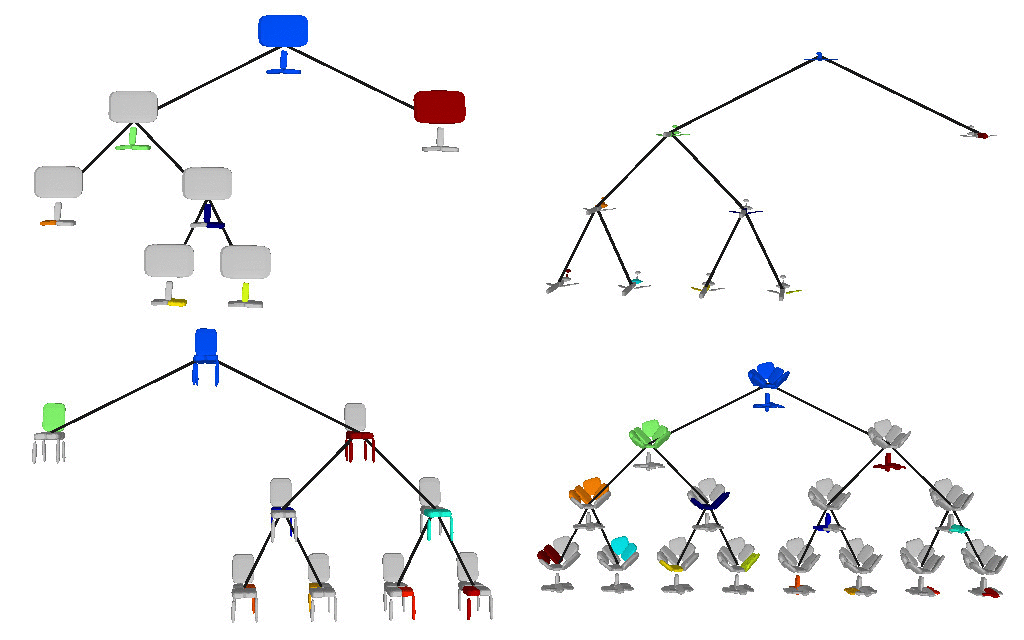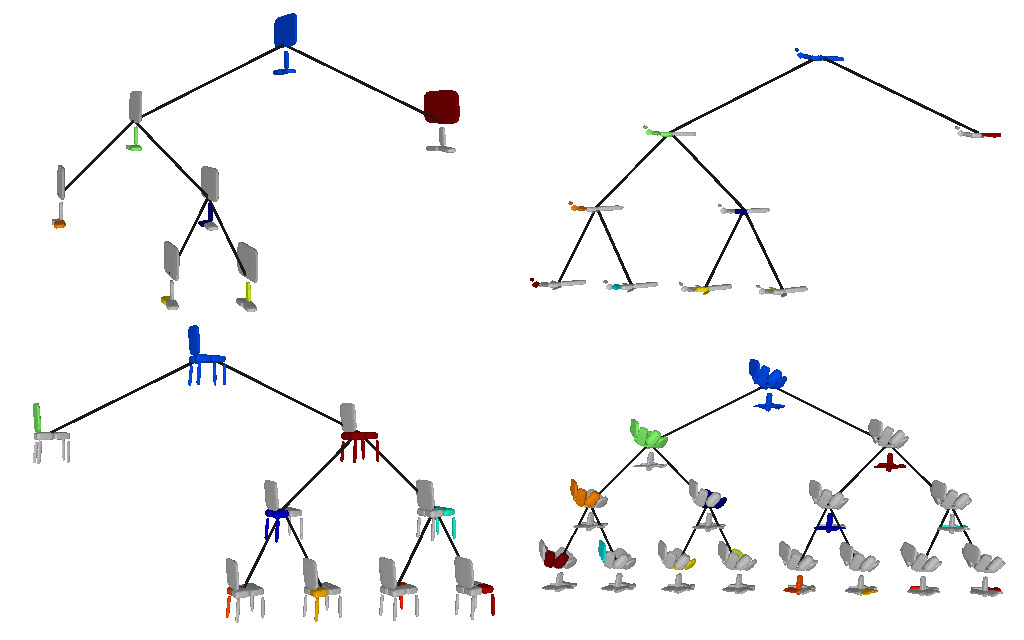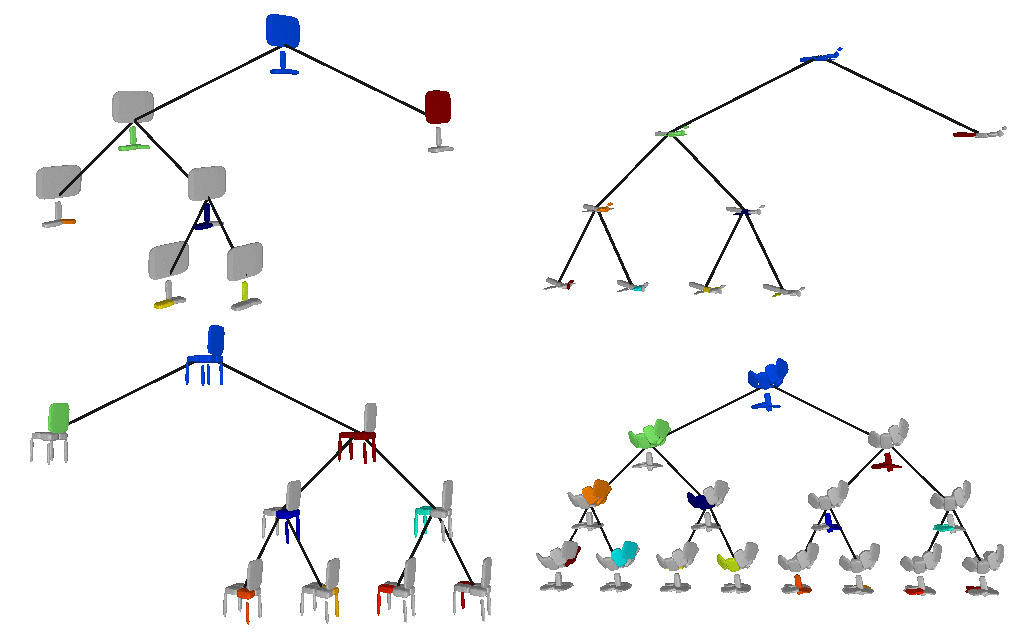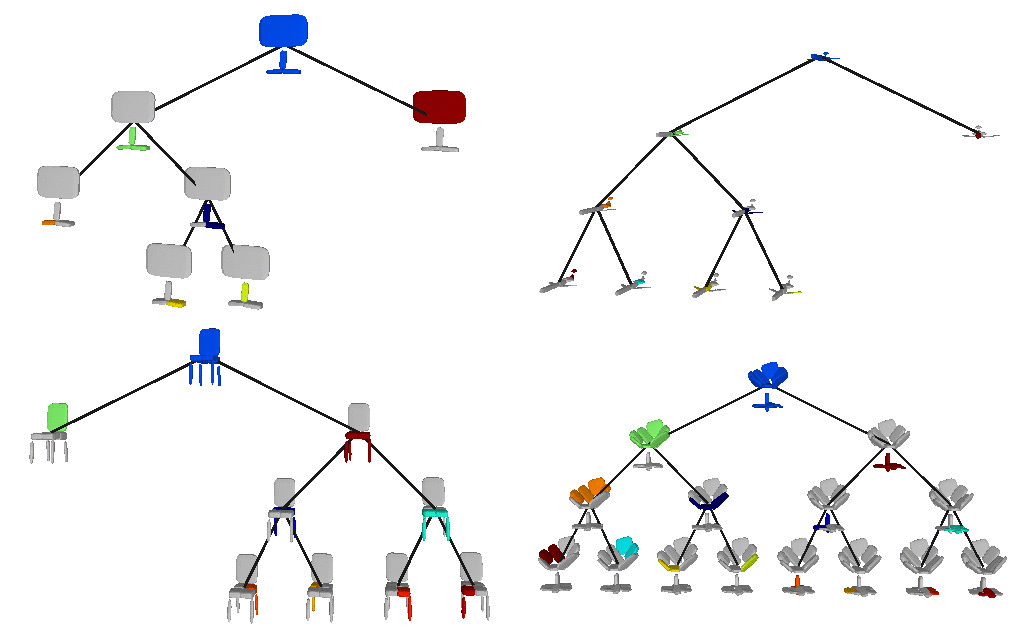
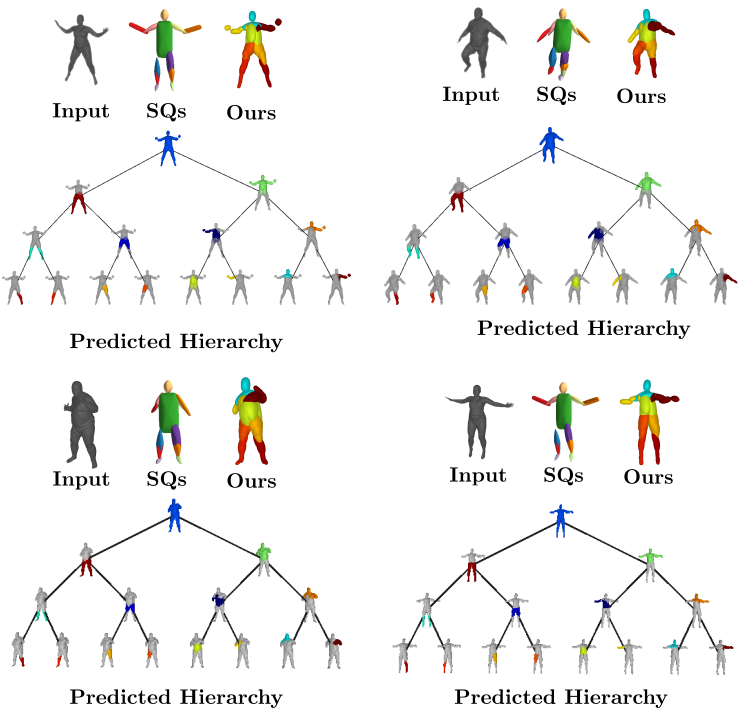
We also validate our model on the Dynamic FAUST dataset, which consists of various humans under different poses. We observe that our structure-aware representation yields geometrically accurate shape abstractions.

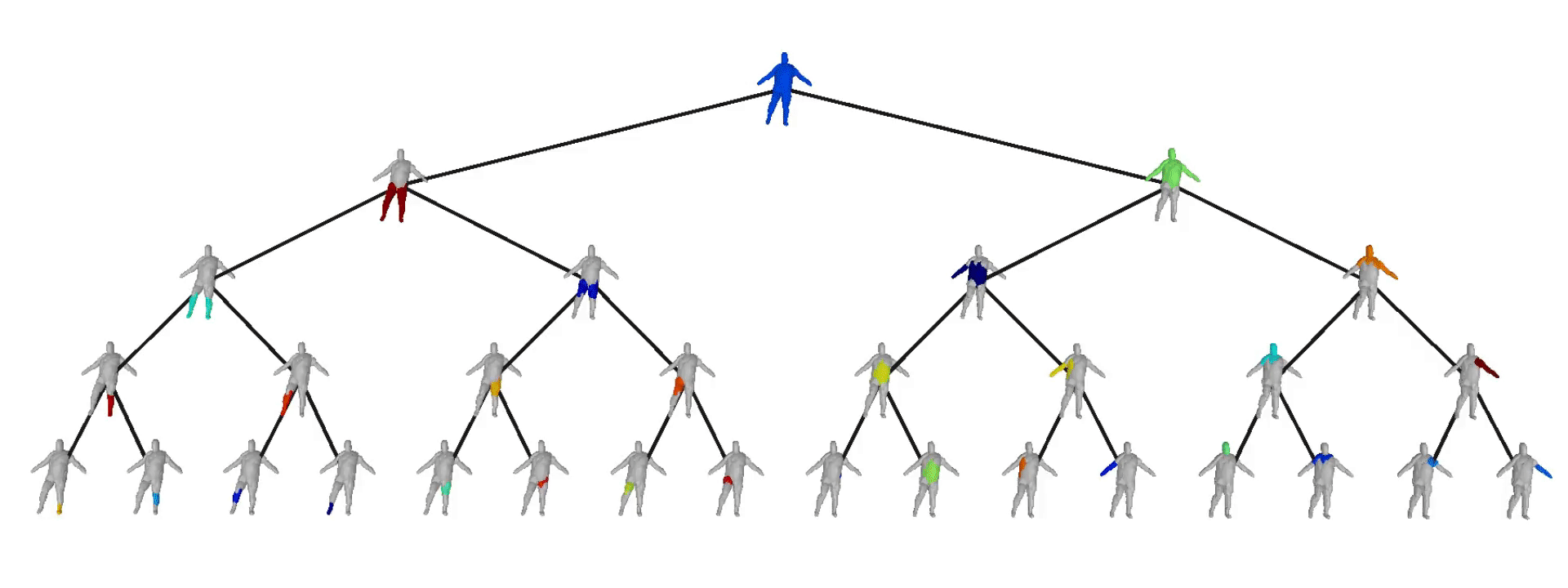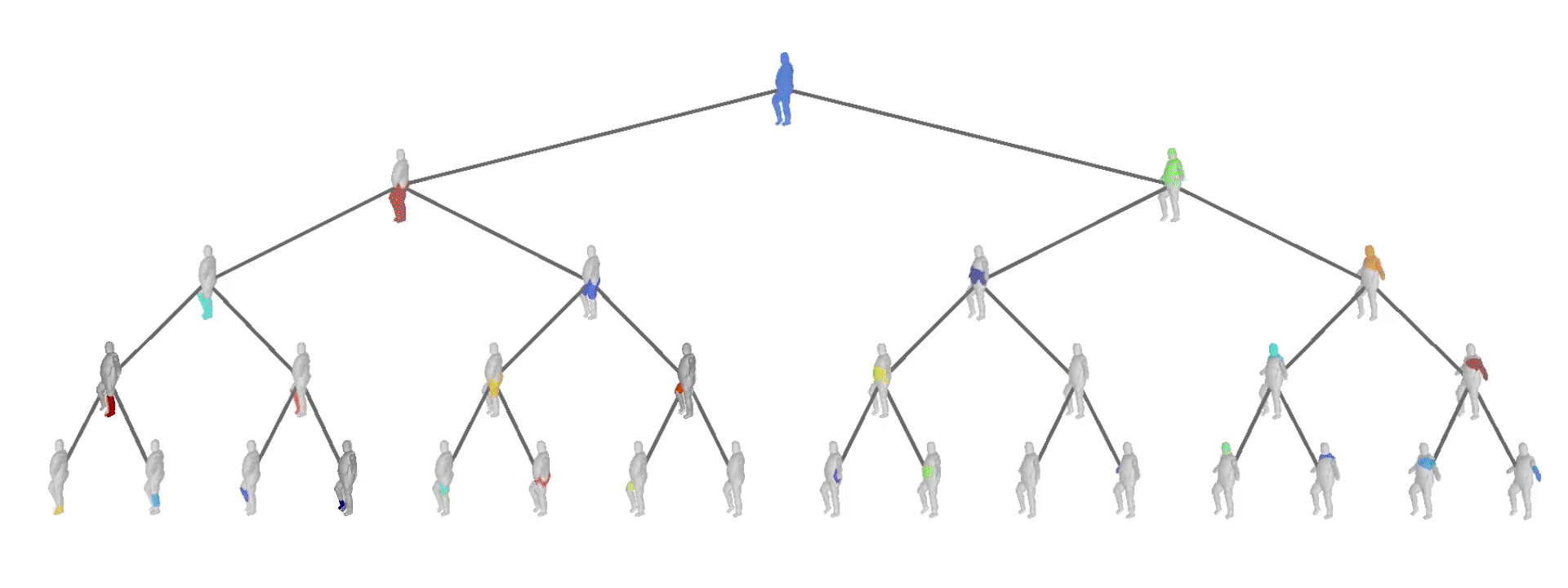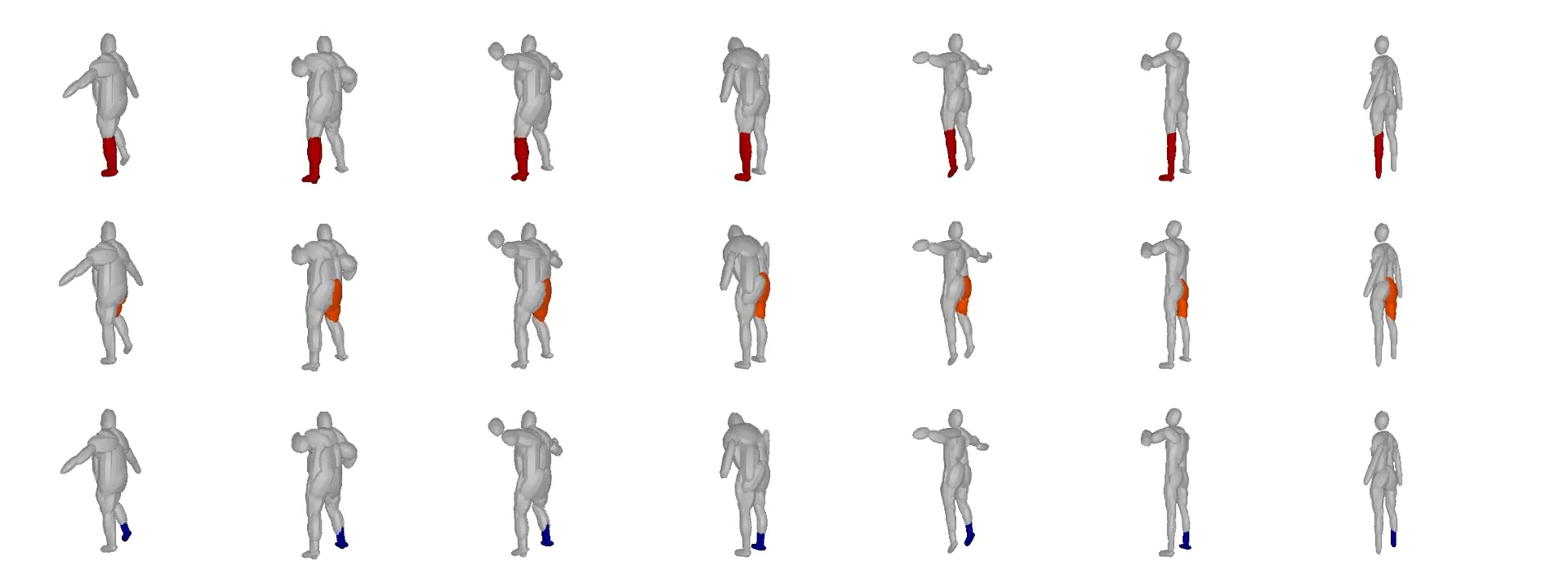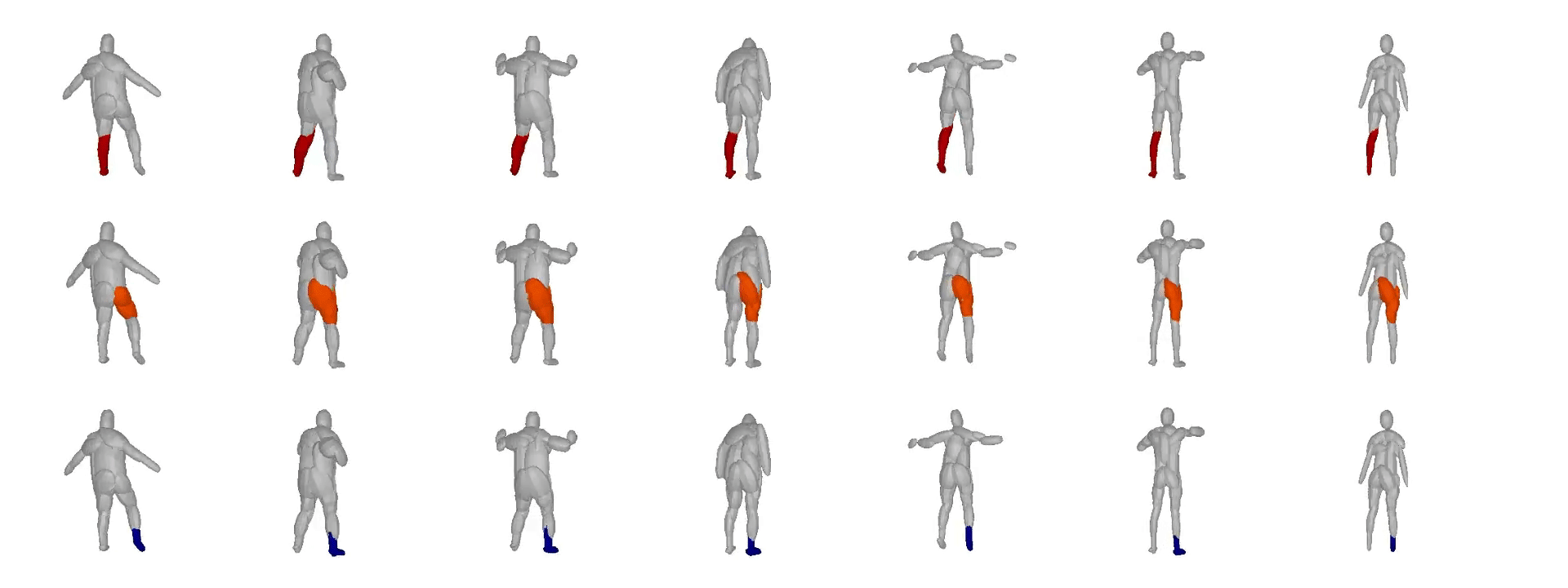
We further observe that our learned hierarchies have a semantic interpretation, as the same node is consistently used for representing the same object part. For example, the node (4, 3) is consistently used for representing the right leg of different humans under various poses (illustrated with blue), while node (4, 12) is used for representing the head of different humans (illustrated with light green).

Further Information

To learn more about work, check our video here:

For more details check out our paper and our supplementary. Additional results for various ShapeNet objects as well as D-FAUST humans are provided in our project page. If you are interested in experimenting with our model you can clone the source code of our project and train your own models.

@inproceedings{Paschalidou2020CVPR,
     title = {Learning Unsupervised Hierarchical Part Decomposition of 3D Objects from a Single RGB Image},
     author = {Paschalidou, Despoina and Luc van Gool and Geiger, Andreas},
     booktitle = {Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR)},
     year = {2020}
}