Automatically, abstracting 3D shapes into semantically meaningful parts without
any part-level supervision is hard. Existing approaches either lead to semantic
abstractions with few simple shapes (eg. superquadrics) or they yield
geometrically accurate reconstructions with a large number of primitives, while
sacrificing semantic interpretability, namely primitives do not represent
identifiable parts. In this work, we attempt to combine the simplicity and
semanticness using an expressive flow-based 3D primitive representation which
enables efficient computation of both the implicit surface function and the
mesh.
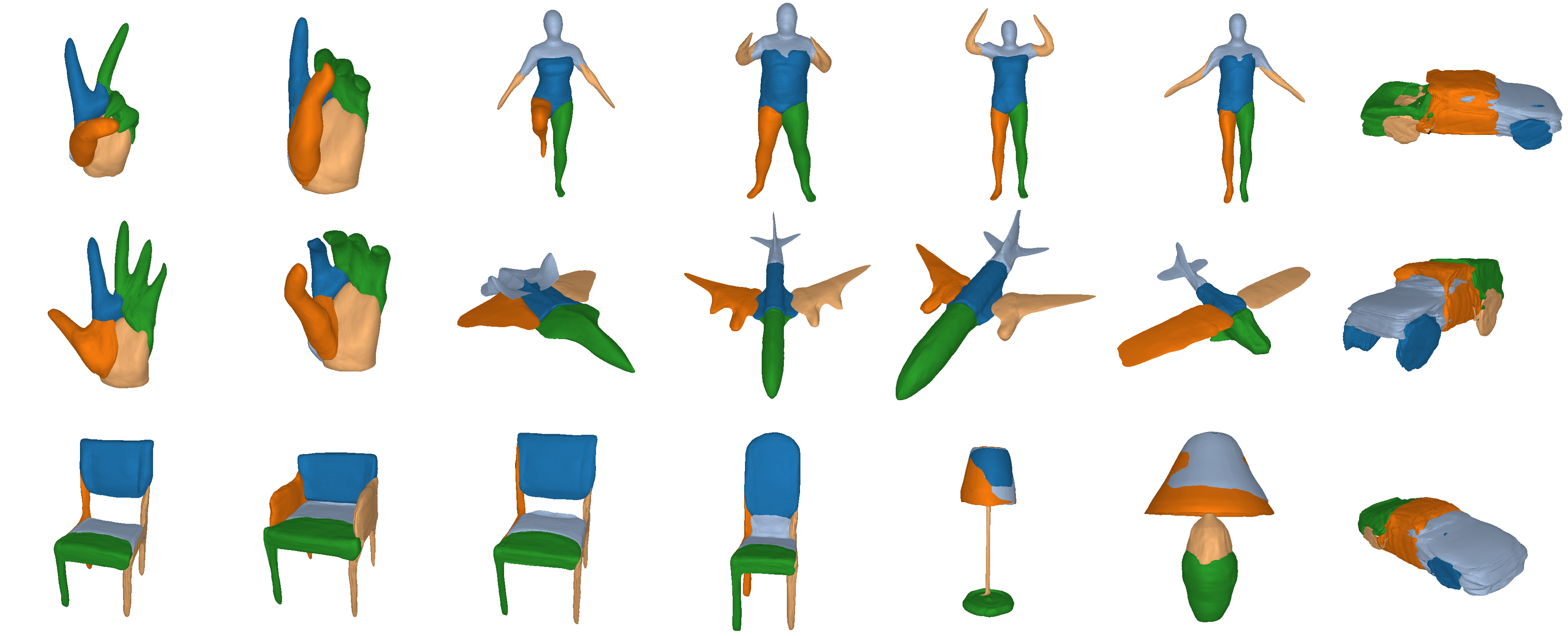Our expressive 3D primitive representation allows to parse 3D objects into
geometrically accurate and semantically consistent part arrangements without
any part-level supervision. Here, we show the reconstructed primitives on
various ShapeNet objects, D-FAUST humans and FreiHAND hands using only 5
primitives.
Our key insight is that a primitive should be a non trivial genus-zero shape with well defined implicit and explicit representations. These two characteristics are crucial in order to allow us to efficiently combine primitives and accurately represent arbitrarily complex geometries.
Why wasn’t this possible before?
Existing primitive-based representations seek to infer semantically consistent
part arrangements across different objects and provide a more interpretable
alternative, compared to more powerful representations that focus solely on the
object geometry. They rely on simple shapes such as cuboids, superquadrics,
3D anisotropic gaussians or more general convex shapes for reconstructing the 3D
geometry as a set of parts.
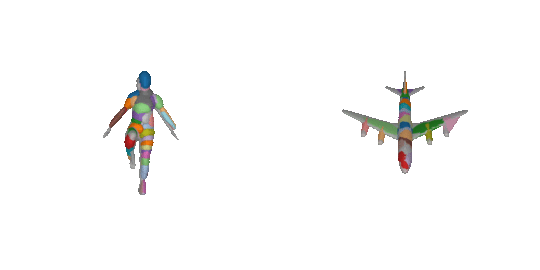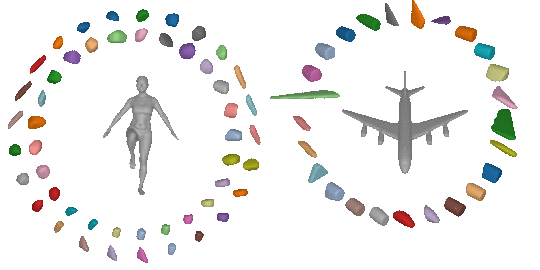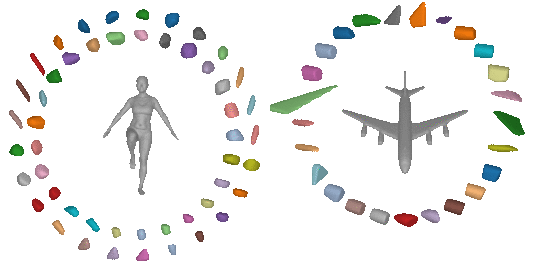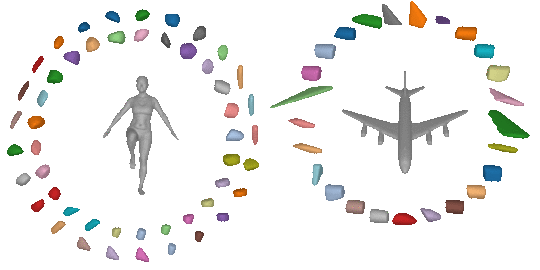Due to their simple shape parametrization, existing primitives require a large
number of primitives to accurately capture the 3D geometry. However, increasing
the number of parts results in less meaningfull abstractions, where parts do
not correspond to identifiable parts.
For example, in the previous image, for the majority of the primitives, it is really hard to say whether a primitive corresponds to a human part or a plane part. This is expected since existing primitives have limited expressivity, due to their simple parameteriazation, namely a primitive cannot represent an arbitrarily complex shape, such the legs the and hands of a human using a single primitive. As a result, in order to represent complex geometries existing primitive-based representations that rely on simple shapes, require a large number of primitives that do not correspond to semantically meaningful parts.
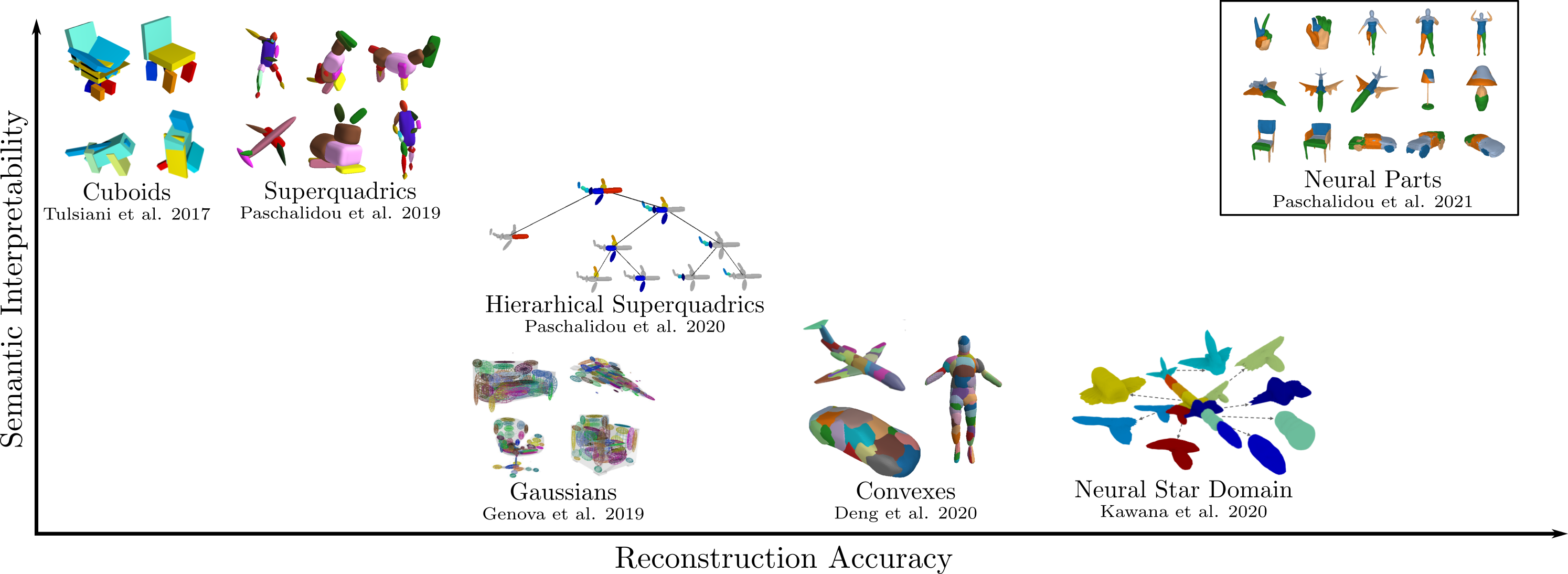Existing primitive-based representations can be arranged based on their semantic
interpretability, namely whether the reconstructed primitives have a semantic
interpretation, and their representation power, namely whether the
reconstructed shape is geometrically accurate. We identify that there exists a
trade-off between the reconstruction quality and the number of parts in
primitive-based methods and we propose a novel primitive-based representation
that addresses this trade-off.
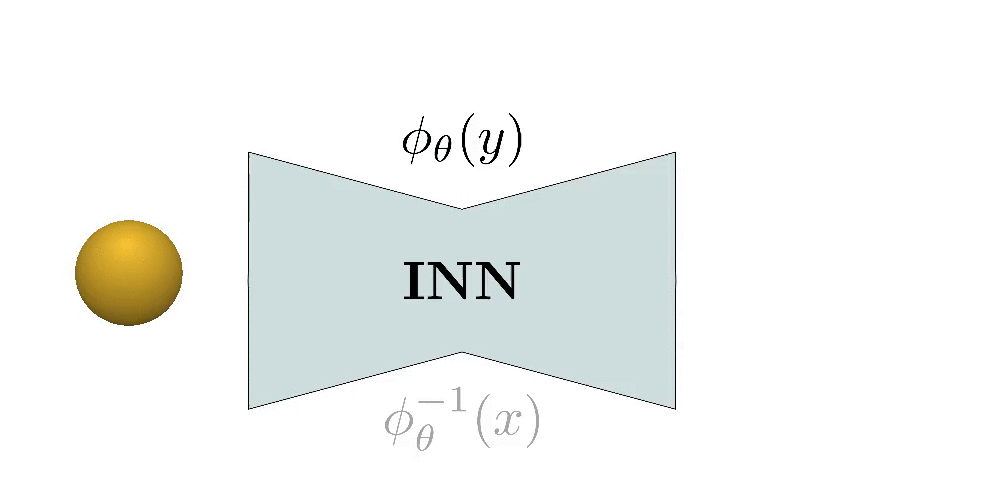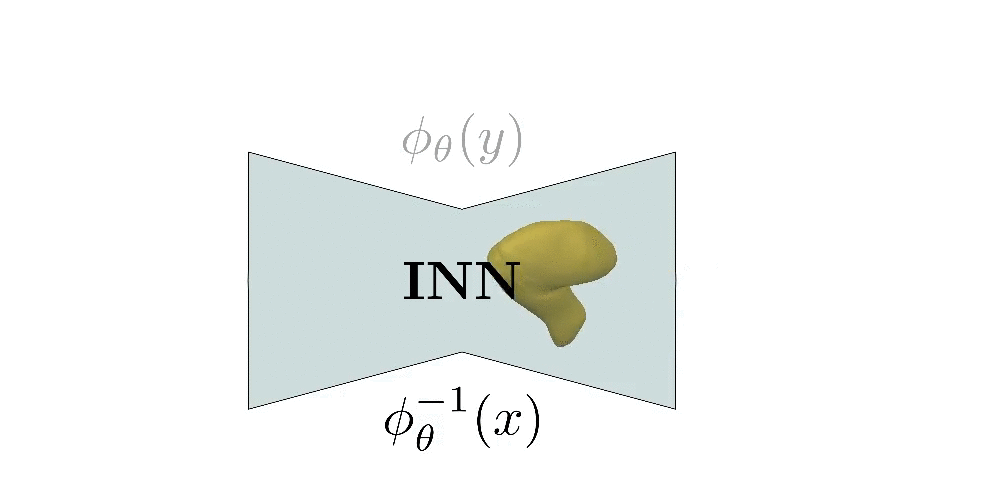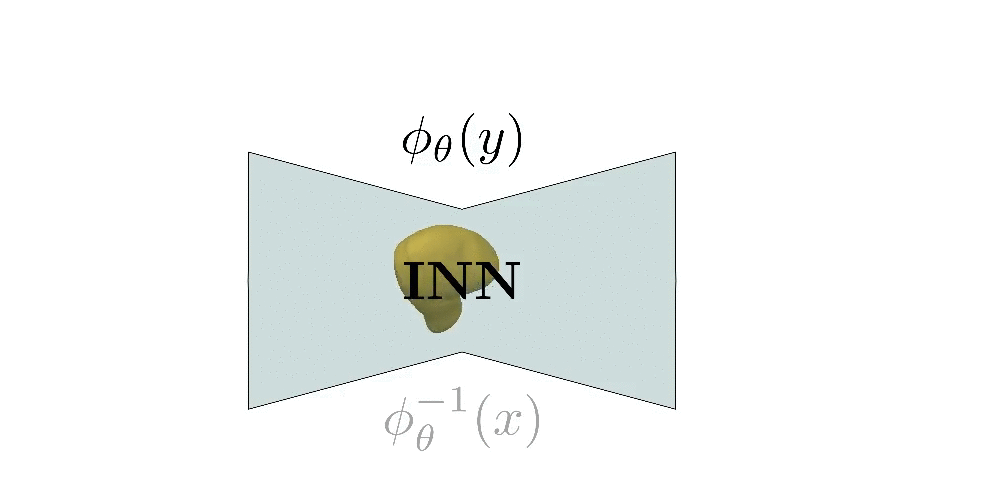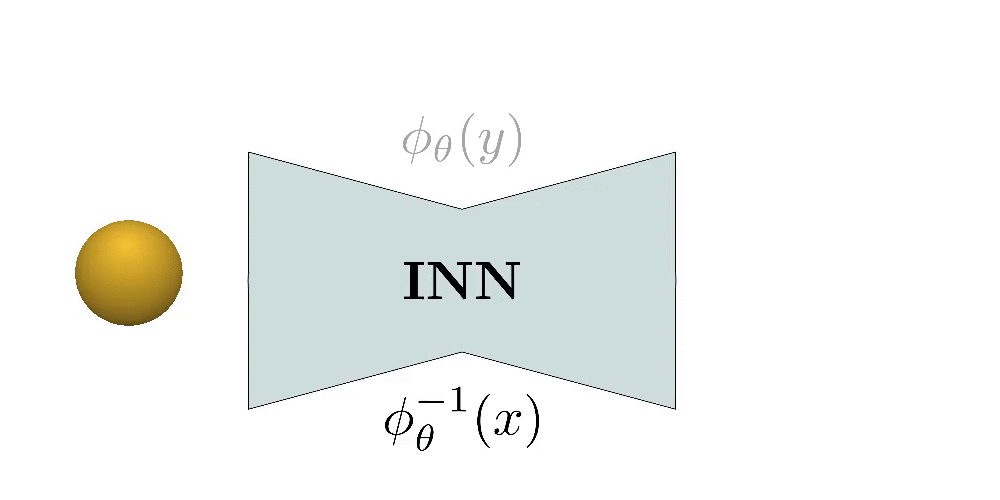
In contrast to prior work that considers convex shapes as primitives, we
propose to define primitives using an Invertible Neural Network (INN) which
implements homeomorphic mappings between a sphere and the target object. The
INN allows us to compute the inverse mapping of the homeomorphism, which in
turn, enables the efficient computation of both the implicit surface function
of a primitive and its mesh, without any additional post-processing.
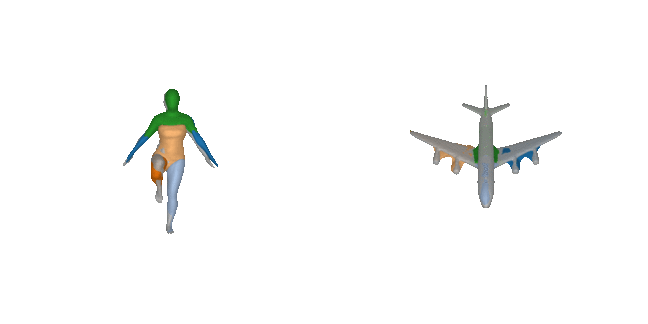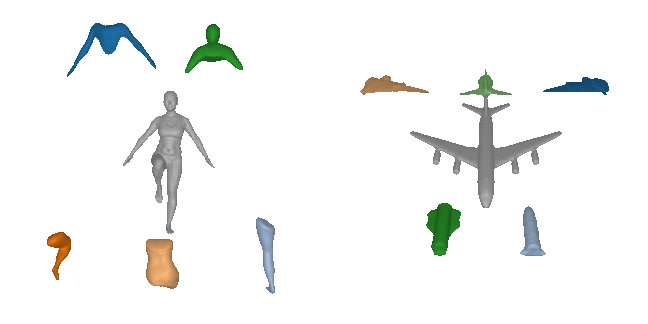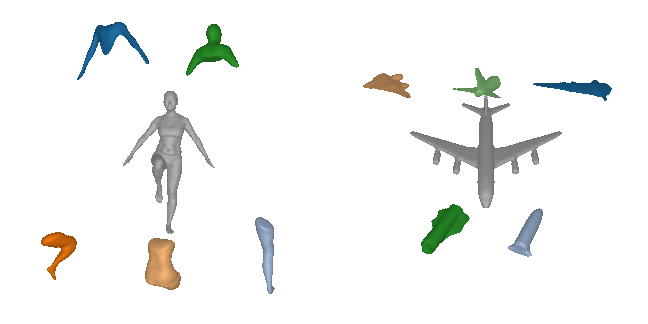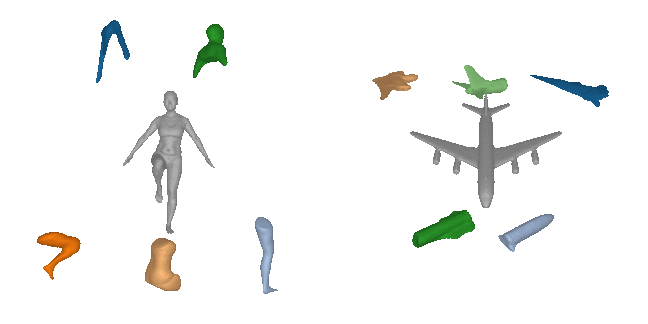
Our Approach
Our main idea is to define each primitive as the deformation of a sphere that
is conditioned on the input via a predicted latent vector. This formulation
does not impose any constraint on the shape of each primitive and thus our
primitives can capture arbitrarily complex genus-zero geometries. In particular,
we define this deformation as a homeomorphic mapping between shapes implemented
with an Invertible Neural Network (INN). A
homeomorphism is a continuous map between two topological spaces \(Y\) and
\(X\) that preserves all topological properties. In our setup, a homeomorphism
\(\phi_{\theta}: \mathbb{R}^3 \to \mathbb{R}^3\) and and \(\phi_{\theta}:Y \to
X\), \(\phi_{\theta}^{-1}: X \to Y\) are continuous bijections.
Intuitively a homeomorphism is a continuous stretching and bending of Y into a new space X. Implementing a homeomorphism with an INN allows us to efficiently compute the implicit and explicit representation of the predicted shape and impose various constraints on the predicted parts such as normal consistency, parsimony etc.
Due to the lack of primitive annotations, we train our model by minimizing the
geometric distance between the target and the predicted shape. Our supervision
comes from a watertight mesh of the target object in the form of surface
samples, i.e. randomly sampled points on the surface of the target object) and
occupancy pairs i.e. points inside and outside the bounding boxes that contains
the target object accompanied by their occupancy labels.
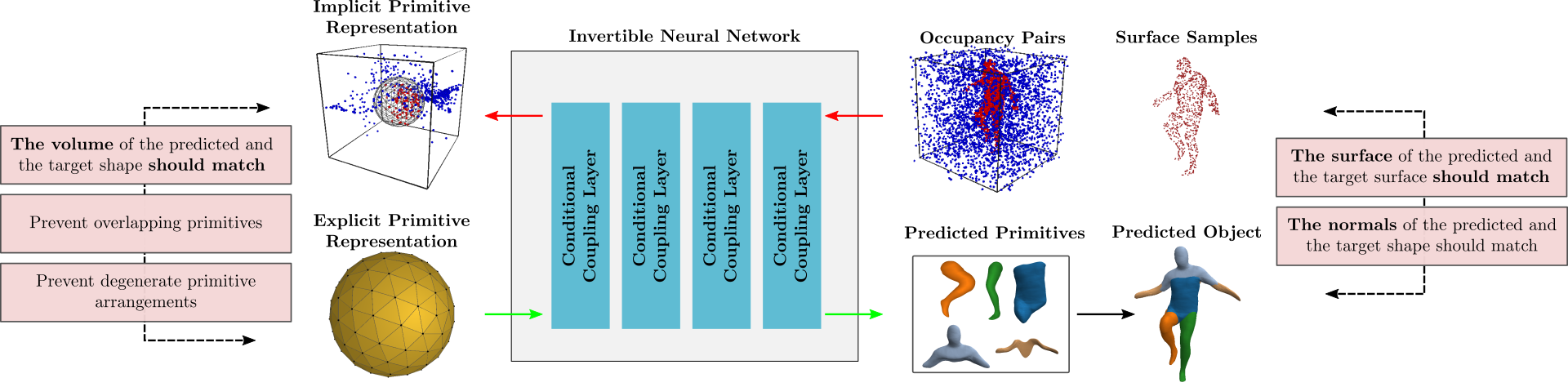
During training, we optimize our network using a Chamfer loss between points on the surface of the predicted shape and the target object, as well as with an occupancy loss that ensures that the free and the occupied space of the predicted and the target shape coincide. Moreover, we define three auxiliary losses that enforce firstly, that the orientation of the normals of the predicted and the target shape is consistent, secondly that primitives do not overlap which ensures that they describe different parts of the object and finally a loss that prevents degenerate primitive arrangements, where some primitives are very small and do not contribute to the reconstruction.
How well do Neural Parts work?
Here, we compare the part-based reconstructions with different number of
primitives using Neural Parts and
CvxNet. Neural Parts accurately capture
the 3D geometry of the human using even a single primitive, whereas CvxNet
fail to capture the 3D geometry even when increasing the number of parts to 10.
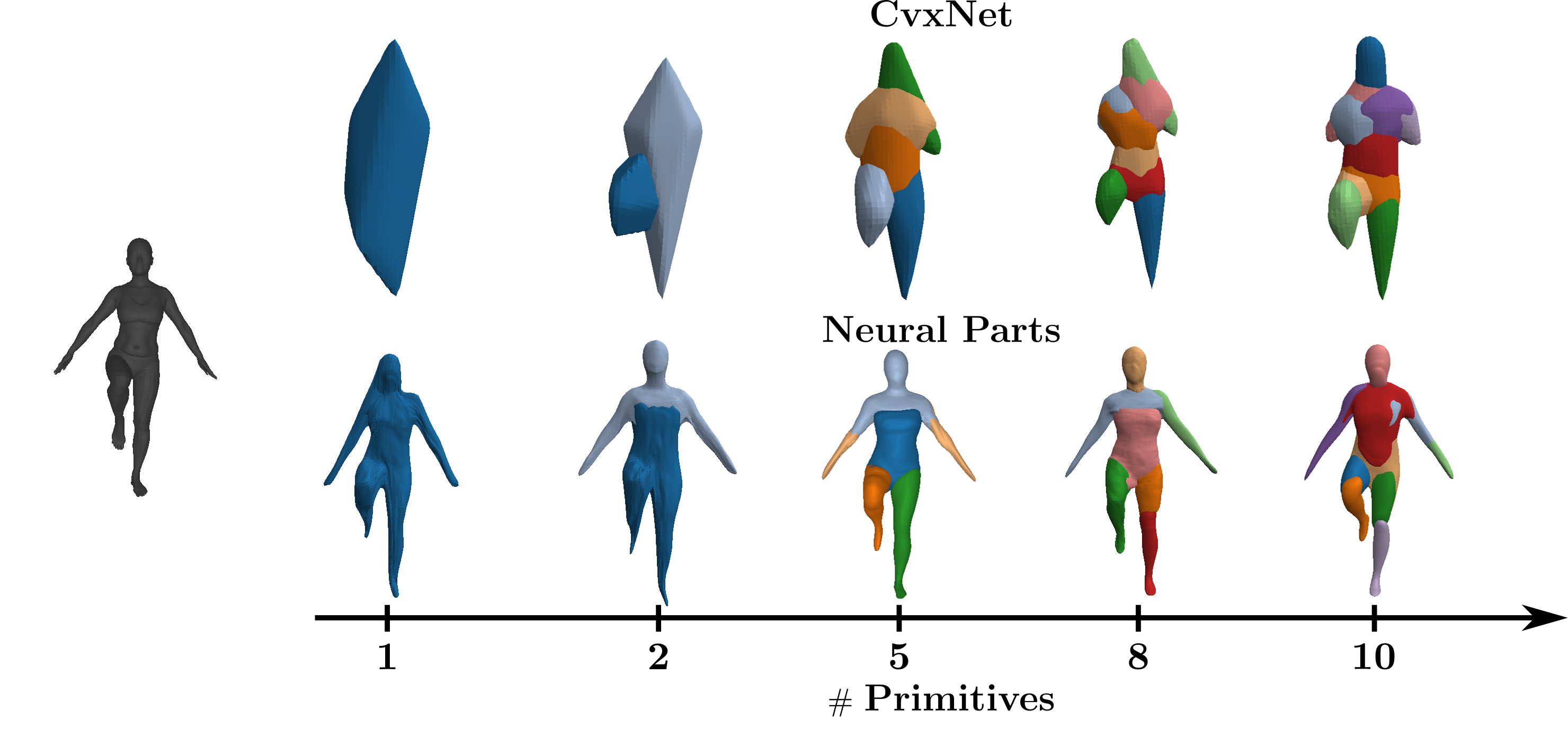For Neural Parts, it can be easily seen that reconstructions with 5, 8 and
10 primitives are very similar, namely Neural Parts achieve similar performance
regardless of the number of primitives. This is a very important property as it
allows us to select the appropriate abstraction level based on our application
without having to compromise abstraction to improve reconstruction.
We evaluate our model on the 3D reconstruction task on the D-FAUST dataset and show that
Neural Parts result in semantically more meaningful abstractions, such as legs and
arms, using only 5 primitives, whereas simpler primitives such as CvxNet,
SQs and H-SQs
require an order of magnitude more parts to accurately represent the
target object. As a result, simpler primitive representations yield less
meaningful abstractions.
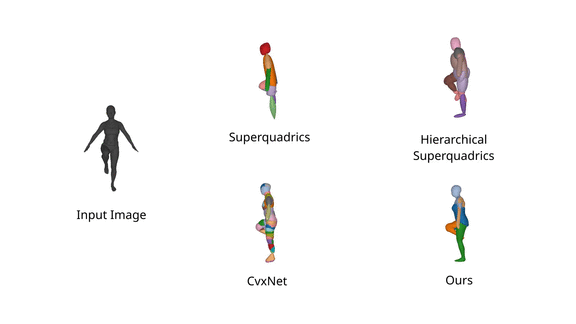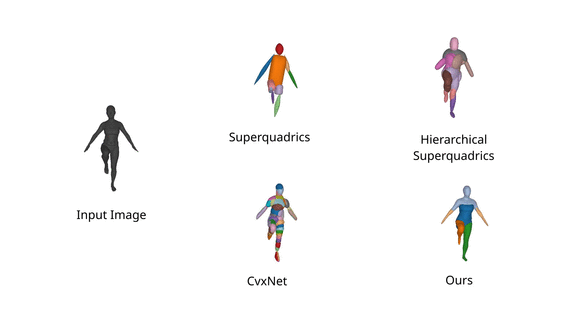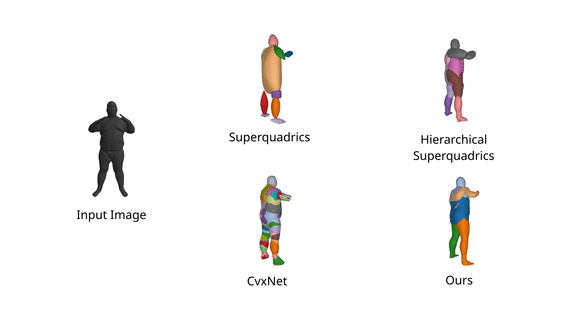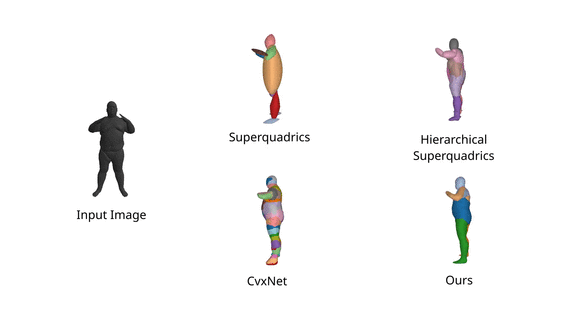In addition, we also note that Neural Parts preserve their semantic identity
through a wide range of human motion, since the same primitive is consistently
used for representing the same human part while humans are moving.
We further evaluate our model on FreiHAND
dataset, and observe
that it faithfully captures fine details of organic shapes such as bent fingers
using a single primitive, while prior work focuses primarily on the structure
of the predicted shape and misses out fine details such as fingers.
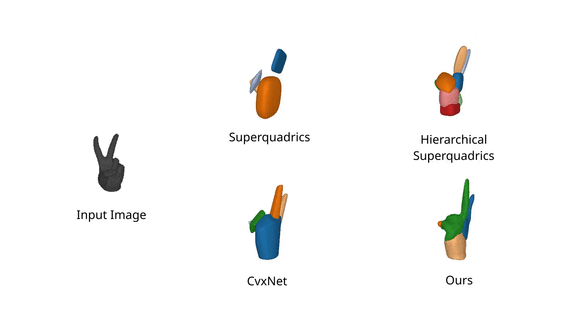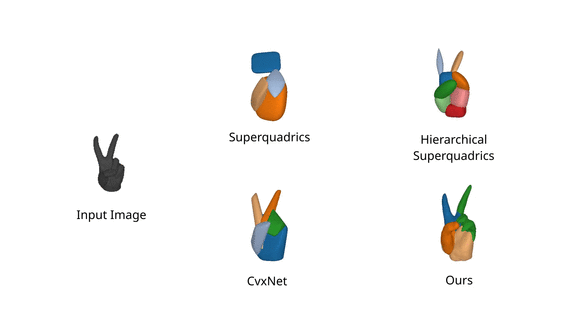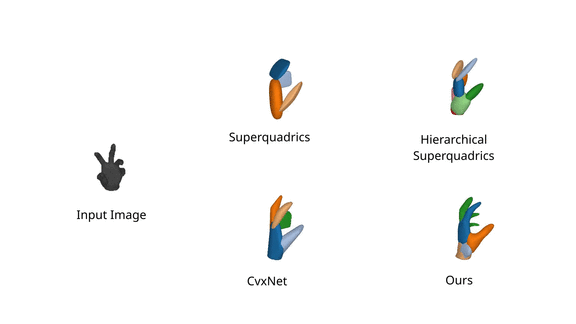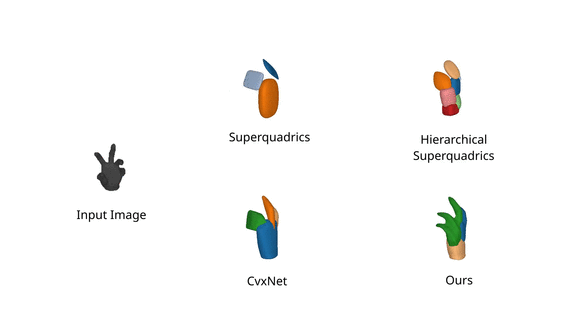
We finally validate our model on various ShapeNet
objects and observe that it results in more accurate reconstructions than
CvxNet with 5 primitives. When increasing the number of primitives to 25,
CvxNet improves in terms of reconstruction quality but the predicted primitives
lack a semantic interpretation.
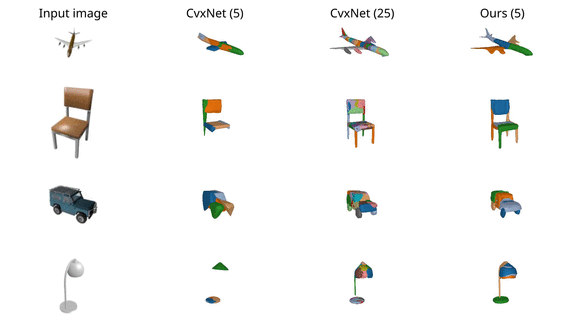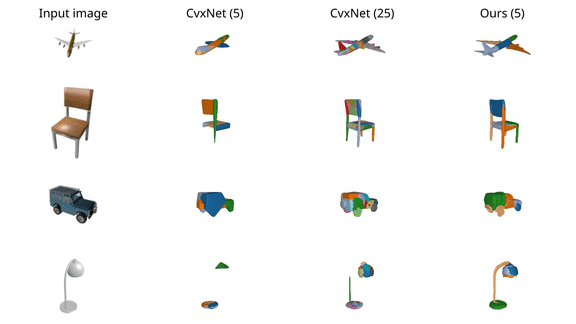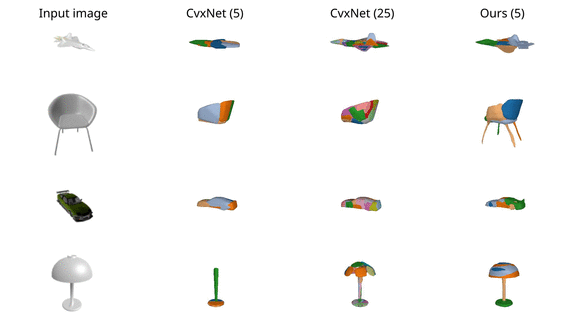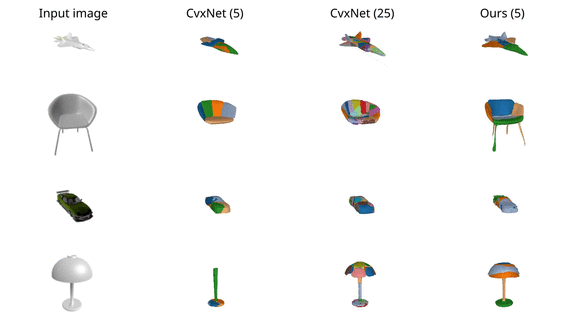For the case of chairs and lamps, CvxNet with 5 primitives do not have enough
representation power, thus entire object parts are missing.
Further Information
To learn more about our work, check our video here:
More information (including the paper, and the code and our pretrained models is available on our project page. Make sure to check out our interactiva demo for visualizing the reconstructed primitives!
@inproceedings{Paschalidou2021CVPR,
title = {Neural Parts: Learning Expressive 3D Shape Abstractions with Invertible Neural Networks},
author = {Paschalidou, Despoina and Katharopoulos, Angelos and Geiger, Andreas and Fidler, Sanja},
booktitle = {Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR)},
month = jun,
year = {2021}
}
