DeFuSR: Learning Non-volumetric Depth Fusion using Successive Reprojections

In many fields of data processing, computer vision included, deep learning is throwing top approaches from their throne. In computer vision, the current wave of deep learning has started mostly in image classification. Beginning with relatively easy recognition problems (does this image show a dog or a cat?), networks quickly became better at classifying subspecies than most humans. Whereas hand-crafted techniques for classification can only leverage the knowledge of their creators, neural networks distill decision rules directly from data; perfect in the case of classification, where the optimal decision rules can be incredibly complex and are typically not known in advance.

Starting from 2015, Dosovitskiy and others demonstrated that deep learning can also be applied to dense correspondence estimation tasks such as optical flow or stereo. While optical flow and stereo can be addressed using image based networks with 2D convolutions, extending these results to the multi-view case where computation takes place in 3D space is a difficult task. In particular the large memory requirements of 3D deep networks limit resolution and therefore also accuracy. In Learning Non-volumetric Depth Fusion using Successive Reprojections, we suggest an alternative approach: Instead of performing computations in 3D space, we successively “fold” 3D information back into the original 2D image views, combining prior knowledge about multi-view geometry and triangulation with the strength of deep neural networks. This allows us to iteratively obtain consistent 3D reconstructions while all computation is performed in the 2D image space.

Multi-view Stereo

In multi-view stereo, we are interested in estimating the 3D structure of a scene based on multiple images of that scene. In the most simple case, the locations $\tilde{u}_1$ and $\tilde{u}_2$ at which two different cameras observe object $x$ can be used to triangulate the object’s location:

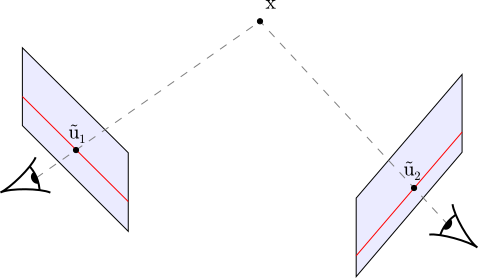
Before being able to triangulate object $x$ based on the input images, we must of course determine the corresponding locations $\tilde{u}_i$ in the input images. The multi-view stereo pipeline is an established approach to this problem:

1. Feature Description
   In the first step, we describe the different possible locations in the images (the pixels) with a feature vector each. The implication/assumption is that, if the feature description of two image locations $\tilde{u}_1$ and $\tilde{u}_2$ are similar, they belong to the same 3D object and can be used for triangulation.

2. Cost Volume Calculation
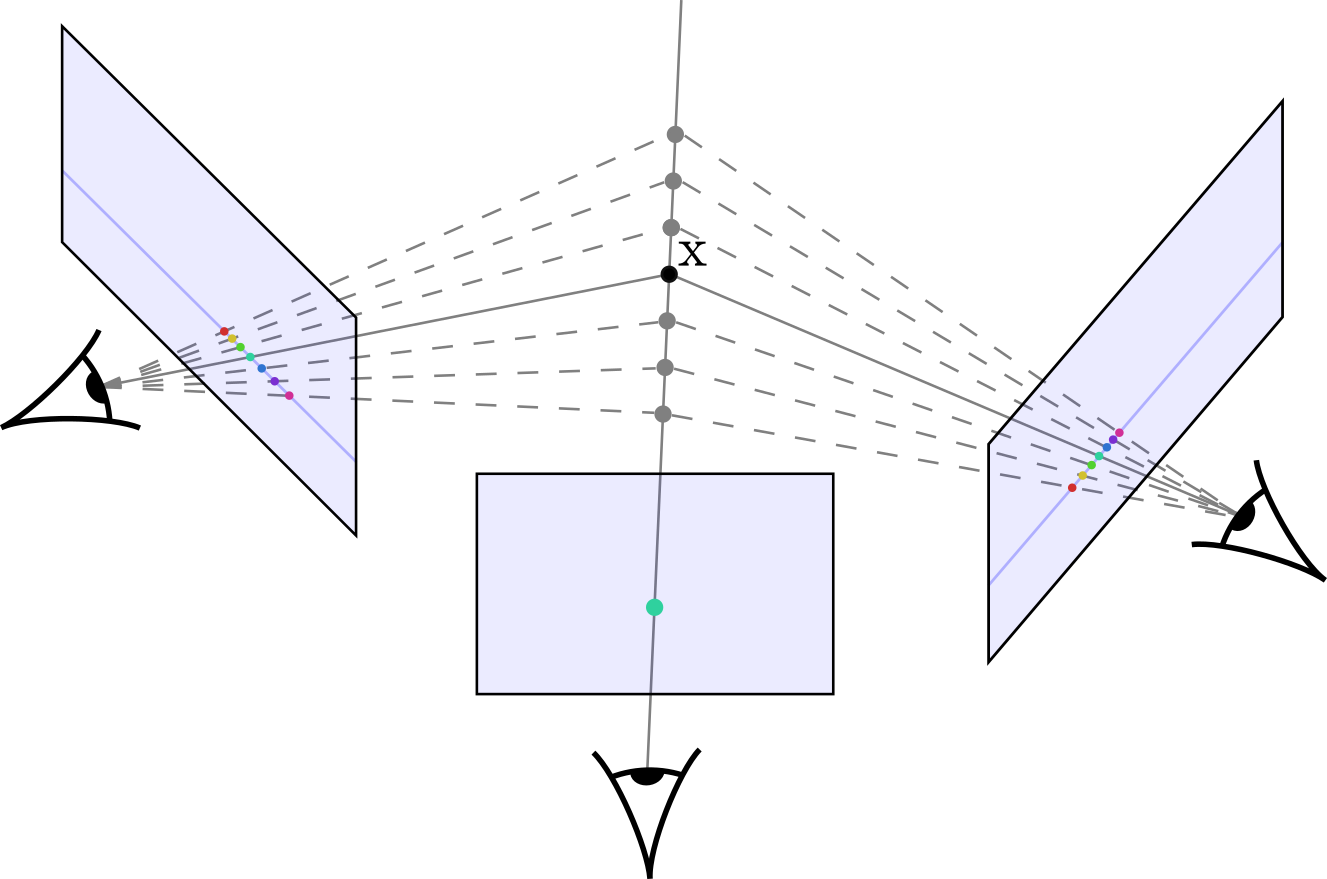
   For a set of 3D positions, we compare the set of all possible corresponding feature descriptions in the other views. If the cost is low, they are similar and likely describe the same surface point. Often, the set of 3D positions is chosen based on a center view: in this case, we draw a line (ray) through each point of interest, and compare the features corresponding to each depth hypothesis with each other – a technique called planesweeping. This is illustrated in the figure below.

3. Depth Estimation
   Performing step 2 for all pixels in the center view and all depth hypotheses yields a 3D cost volume from which the most likely location along each ray can be determined. Often, the resulting estimates are noisy and therefore need to be filtered or smoothed by exploiting the fact that depth is smooth nearly everywhere a few exceptions at sharp edges or object boundaries.

4. Depth Fusion
   To arrive at a complete 3D representation of the scene all resulting triangulated points $x$ can be fused into one 3D reconstruction. However, even after filtering and smoothing the estimates, the result often contains a large degree of noise and inconsistencies. Traditional techniques therefore leverage various heuristics to arrive at a consistent 3D reconstruction. The most common assumption is that each 3D point $x$ must be supported by 3D points triangulated from other views in order to be trusted. All points which do not fulfill this criterion are removed.

Deep Learning-based Multi-view Stereo

Various parts of the pipeline described above are currently being replaced by learned alternatives. Neural networks can be exploited for generating distinctive features as shown by Hartmann et al. and MVSNet, among others. An approach that explicitly leverages cost volumes for binocular stereo was presented by Kendall et al. and depth map filtering was demonstrated by, e.g., DDRNet.

The final step, combining the different depth maps into a single scene representation, was also tackled from a learning-based angle. In Riegler et al. we have demonstrated that voxel-based depth map fusion is feasible. However, despite exploiting memory efficient octree data structures, this method was limited to resolutions up to $256^3$ voxels. In this work, we explore depth maps themselves as representation for fusing multiple depth maps. While not as rich as volumetric grids, depth maps can be processed efficiently and at comparably large resolution as all computation can be performed in the 2D image domain.

Our Fusion Approach

After performing planesweeping for all views, we iteratively consider each view as the center view. To leverage the information of neighbouring views, we reproject depth and feature information from all neighbours which share a similar field of view onto the center view. These reprojections are then used to refine the initial depth estimate from planesweeping:

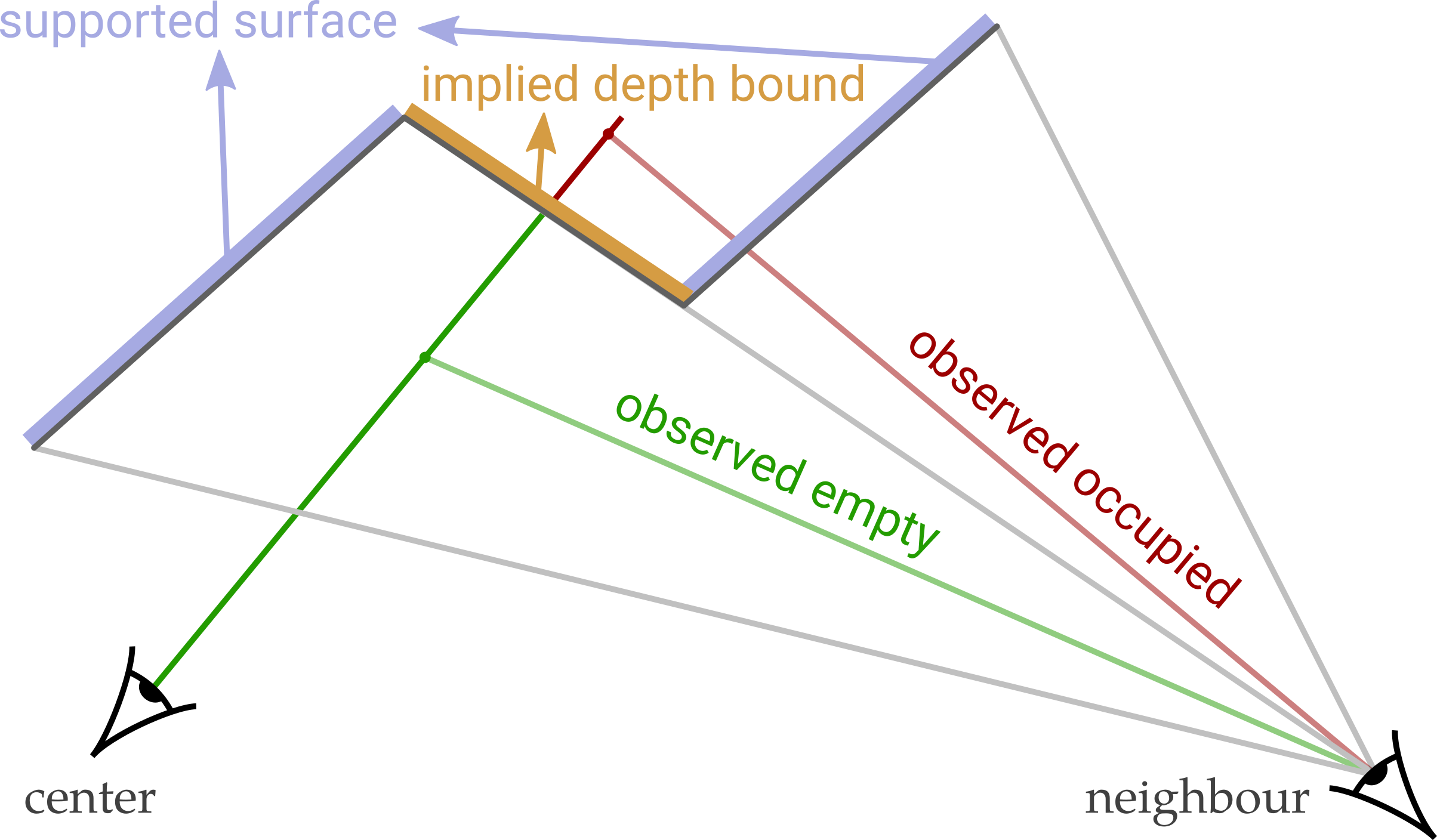
As illustrated below, there exist two types of information we can obtain from a neighboring view. (1) the surfaces that the neighbor observes and which support the depth map of the center view (blue). (2) the depth boundaries implied by depth edges in the neighbor’s depth map (orange). This second cue allows the center view to eliminate depth hypothesis closer than the orange line which would disagree with the depth map predicted of the neighbor.

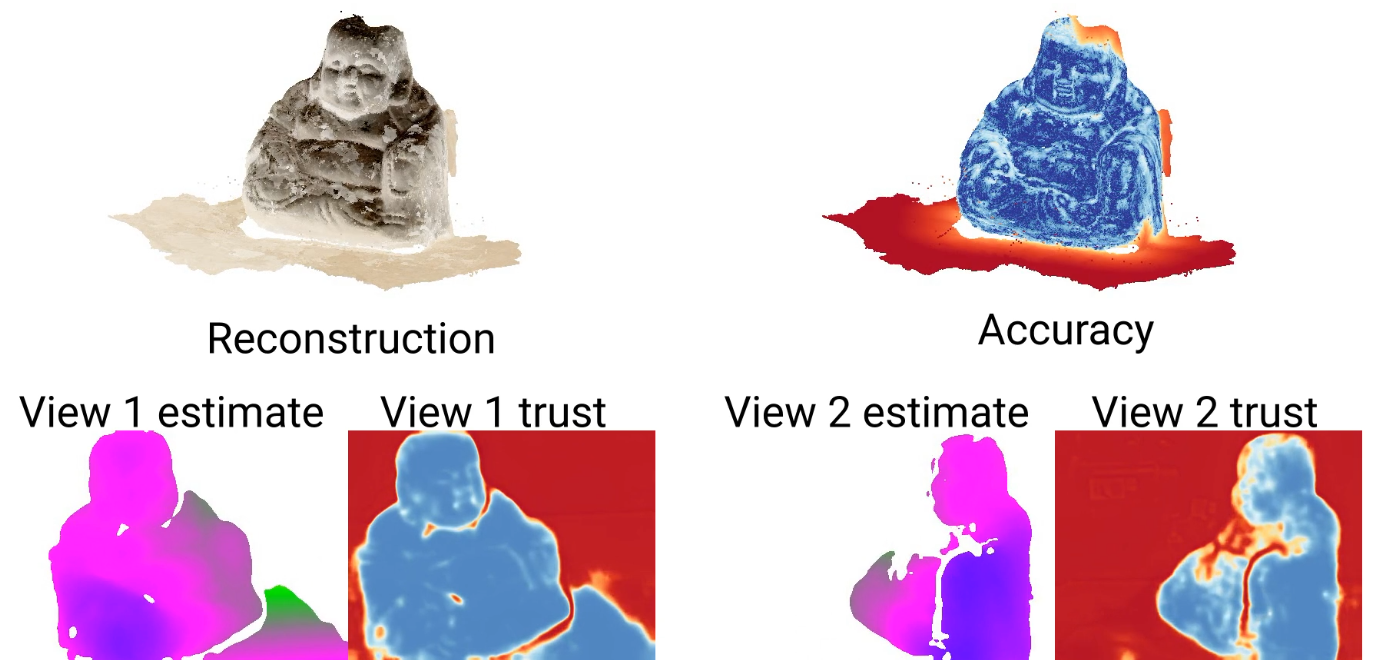
The original depth estimate as well as the input image, and the reprojected information from the neighbors, is fed into a neural network that returns both an improved depth map and a confidence estimate for this new depth map.

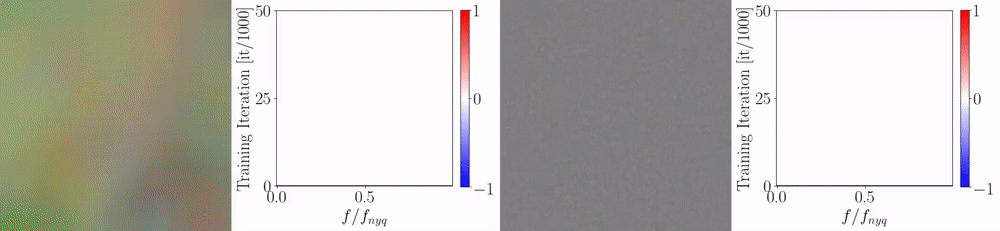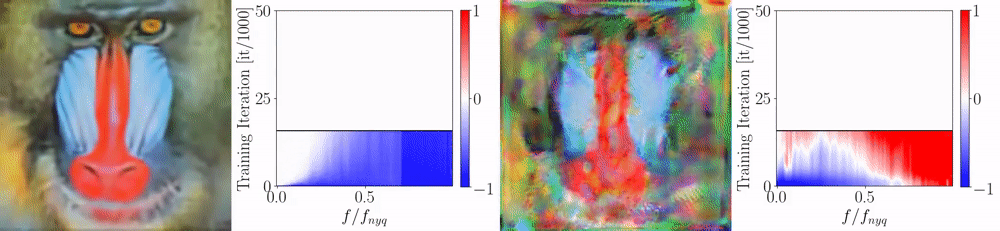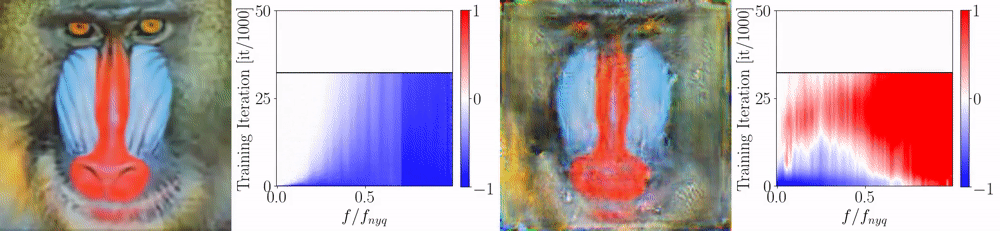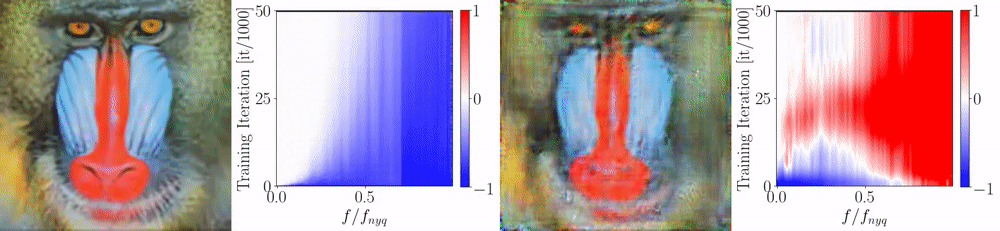
We perform multiple rounds of this depth fusion approach in an auto-regressive fashion. As after each iteration, all depth maps improve, the neighbor information in subsequent iterations is of higher quality. In practice, the performance quickly saturates and we found that three iterations over all views are sufficient. Below, we show the resulting depth error in terms of the iterations, for depth maps estimated by two different techniques (COLMAP and MVSNet). Blue colors indicate low errors and red colors represents large errors. Note how quantization artifacts (for MVSNET) and errors are reduced while applying the proposed fusion technique.

Finally, we demonstrated that the proposed approach also works with data different from the data the network was trained on (different camera, object types and environment).

Further Information

To learn more about DeFuSR, check out our video here:

You can find more information (including the paper, code and datasets) on our project page. If you are interested in experimenting with our approach yourself, download the source code of our project and give it a try. We are happy to receive your feedback!

@inproceedings{DeFuSR,
    title = {DeFuSR: Learning Non-volumetric Depth Fusion using Successive Reprojections},
    author = {Donne, Simon and Geiger, Andreas},
    booktitle = {Proceedings IEEE Conf. on Computer Vision and Pattern Recognition (CVPR)},
    year = {2019}
}